How to design fractals for 3DPrinting

Using fractals to design complex shapes
Fractals Intro
Fractals are geometric patterns that repeat at different scales. They exhibit the property of “self-similarity”. Fractals appear complex in shape. But they are just iterations of simple geometries in a pattern. Consider an equilateral triangle, inscribe another equilateral triangle within and continue doing this. You will end up with a Seirpinski’s Triangle. This is a simple geometric fractal.
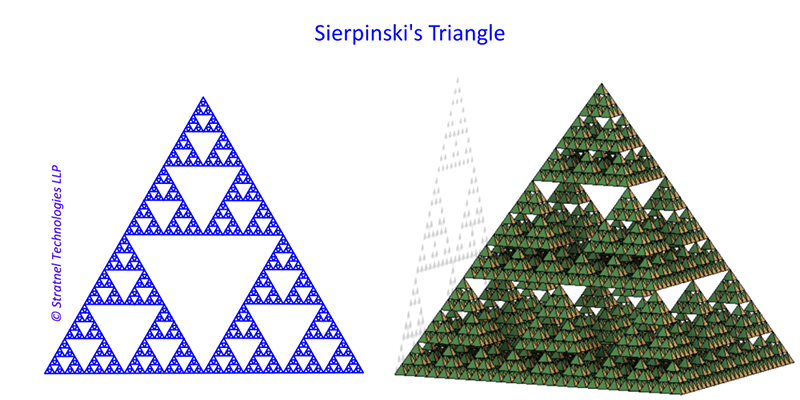
Fractalfoundation.org: “A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems – the pictures of Chaos. Geometrically, they exist in between our familiar dimensions.”
Fractals appear all over nature from microscopic to cosmic scales. The arrangement of cells in living organism and stars show fractal-like patterns. A simple example in your daily life is branches of trees or lightning on a stormy day.
Origin of fractals
The term fractal was first coined by Benoit Mandelbrot in 1975. It derives its origin from the Latin word fract meaning broken or fragmented. Fractals are able to describe complexity in nature better than Euclidean geometry. According to James Gleick ,”In the mind’s eye, a fractal is a way of seeing infinity”- from Chaos (1987), 98. Fractals are powerful tools. Various fields such as architecture, biology, weather modeling, astronomy, networking, digital art, etc. use fractal as a tool.
Application of fractals
Fractals have been applied in several fields of human knowledge including architecture, antena design and mechanical cross section of ropes. Fractals also appear in nature in several locations including the human lungs, propogation of lightning, tree branches and coastlines.
Exploiting fractals in engineering design
3D printing can be used for creating complex shapes. Since shape is not a limitation for 3D printing, fractal design helps in creating complex shapes to solve engineering problems. In here we will be discussing the design aspects and will not be covering the actual 3D printing process by itself.
The principle of fractals can be exploited in engineering design in many ways. Some of the typical examples are weight reduction in structural members, compaction in antenna designs, heat transfer applications, equalised fluid flow paths etc.
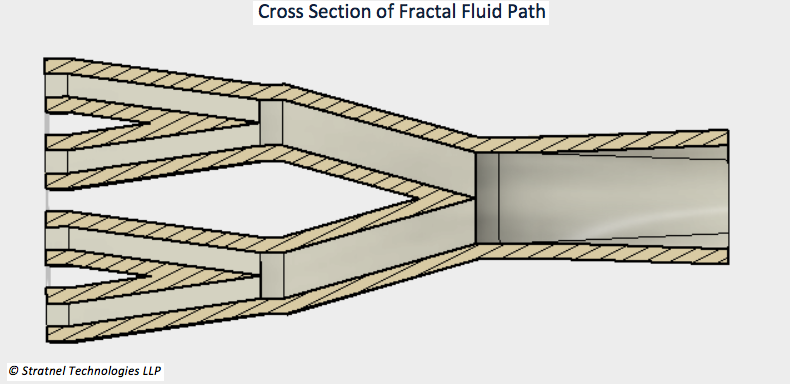
Here is an example for fractal fluid path creation. The objective here is to divide fluid paths in an equalised patterns keeping the overall flow area constant and minimise friction losses to due changes in the flow of length or directions.
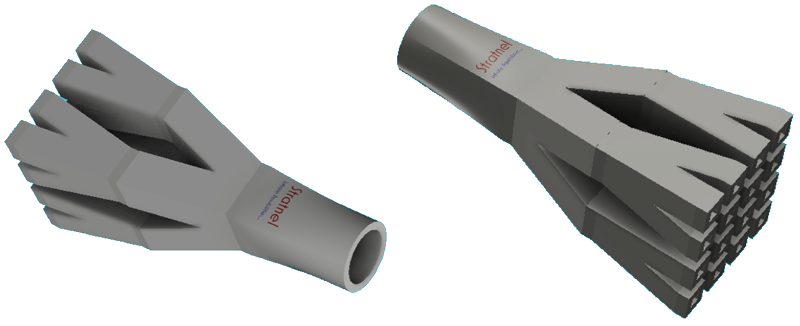
Design steps for creating fractal fluid path
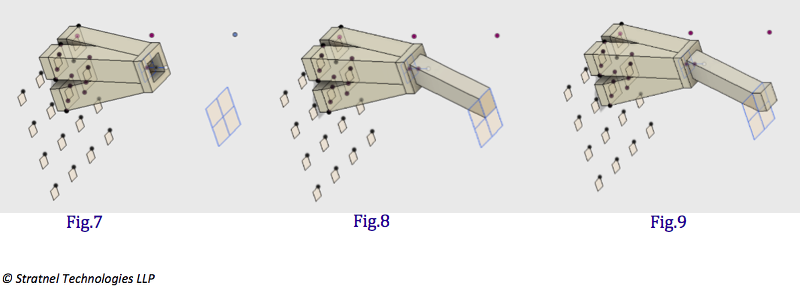
1. I have described the main design steps in Fusion360, without some of the intermediate steps.Create a pattern of 16 nos 3 mm squares in a plane with a pitch of 10 mm between them in X and Y directions ( Fig 1) . Create another plane at a distance of 25 mm in the Z axis. Project the mid point of the 4 shaded squares to the second plane. And draw a square of 6 mm in the second plane with the projected point as the centre (Fig 2). Please note that this is an important step. The 6 mm square will have the same area as the sum of four 3 mm squares. ( 4* 3^2= 6^2) . One could accordingly change the dimensions to suit the application. Loft one of the corner 3 mm squares in the first plane to the corresponding quadrant of the 6 mm square in the second plane. This creates the first fluid passage (Fig 3). The design still has not added any wall thickness, which will come in the subsequent steps.

2.Extrude the top square after lofting by 3 mm. This is done to minimise the impact of direction changes by equalising after every step of the fractal division. (Fig4) . Create a circular pattern around the center axis and create 4 identical bodies of fluid passage (Fig 5). Wall thickness is still not added. The next step is t0 combine the 4 bodies into a single body and shell outward with 2 mm wall thickness (Fig 6). Now we have created 4 flow paths of equal size and flow distance and deflection angles, with wall thickness.

3. The next step will include creating another plane at 25 mm from the top of the body (created above) and draw a square of 12 mm . As explained in step 1 this is to account for the same area as four 6 mm square flow areas. ( 4*6^2= 12^2).(Fig 7). As, before the 6 mm square passage is lofted to the corresponding quadrant of the 12 mm square. ( Fig 8). Again the top surface is extruded by 3 mm.
4. Similar to what was done for Fig 5 in we again create a circular pattern to create 4 bodies. (Fig 10). These 4 bodies are combined and shelled outward with 2 mm wall thickness. (fig 11). The next step is to circular pattern the first set of combined body cluster in Fig 7 around the axis which passes through the center of the 12 mm square.
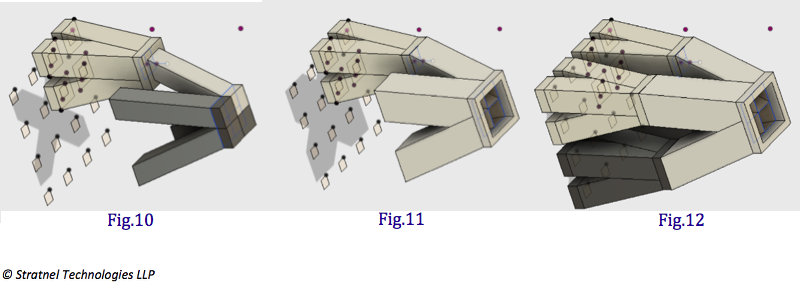
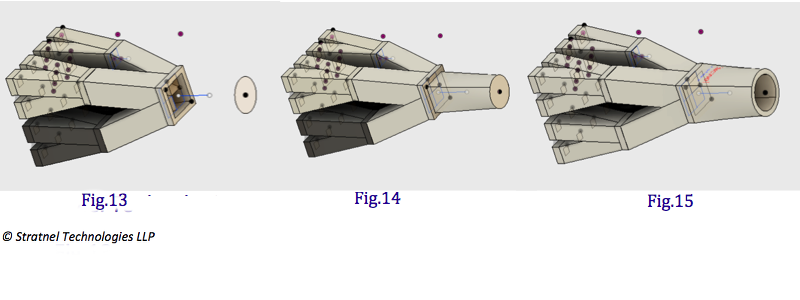
5. We are almost there. We need to add another body to convert the square 12 mm opening to 13.543 diameter opening to again keep the area constant. ( 12*12 = π/4*13.543^2) . This is done to facilitate connection to round pipes. Create an offset plane by 30 mm and draw a circle of dia. 13.543 . (Fig 13). Loft the 12mm square to the 13.543 dia. circle. (Fig 14). The final step is shell the body outward by 2 mm and combine all the bodies (Fig 15) and it is done.
Conclusion
These parts are suitable for 3d printing. One could also add other features to this part like threads and or other features. With such complex shapes, making such a product through any process other than 3D printing involves several limitations including design, machining, patterns, overall costs, etc. 3D printing is elegantly suited for manufacturing such fractal-based designs.
